微分方程式のパラメータ推定

2021年11月10日2022年12月13日

概要

最近また新しく Udemy の講座をつくりまして、その中で微分方程式のパラメータ推定の話をさせて頂きました。要するに与えられた微分方程式のパラメータが未知であるとして、そのパラメータを観測データから推定するといった問題の話です。

講座の方では、ロトカ・ボルテラ モデルという微分方程式を扱っているのですが、講座用に作った例題が余ったので、こちらのブログで紹介しています。

感染症の微分方程式

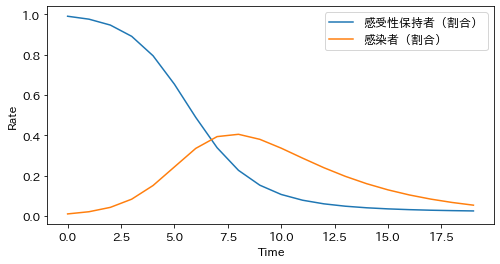
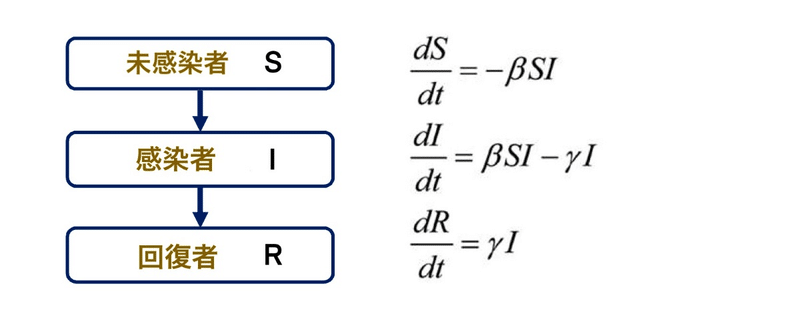
感染症のモデル化に使われる SIR-model にデータをあてはめてみています。微分方程式は S, I, R の比率をコントロールしているものとして、I の比率に応じて感染者が増減する、というモデルにしています。論文等でも紹介されているモデルではあるのですが、個人的にはこのモデルがあまりしっくり来ていないので、講座では使いませんでした。

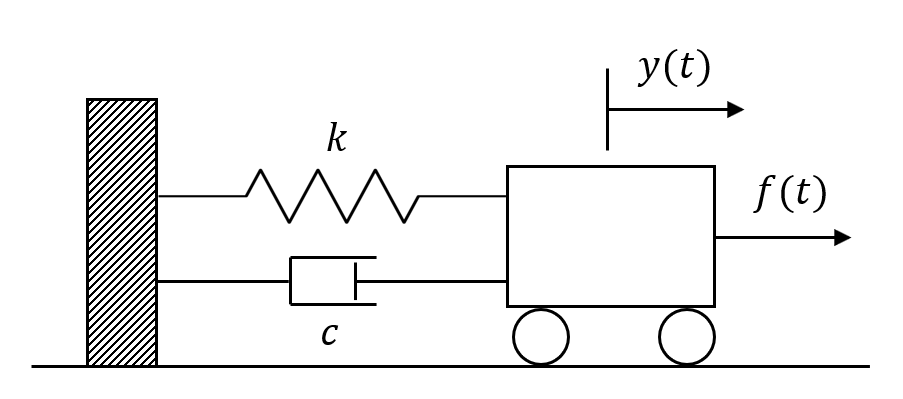
バネマス系での微分方程式

制御の方でよく知られているバネマス系もやってみました。状態空間モデルのようにはうまく外力を設定できないので実用的ではないですが、機械系のバックグラウンドのある方には理解しやすい部分があるかもしれません。

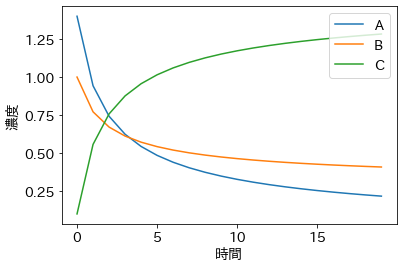
化学反応の微分方程式

化学反応をモデル化した微分方程式でもやってみました。割とうまく行った気がするのですが…

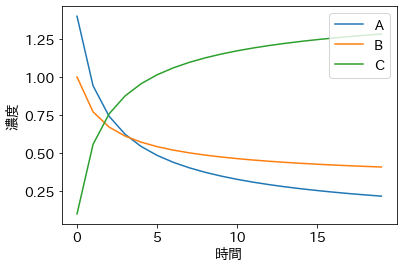
微分方程式のモデル選択

線形回帰のモデルなどでは、複数のモデルがあるときに情報量基準でモデルを選択する、ということをよくやるのですが、それと同じことが微分方程式でもできるかを試してみました。微分方程式は上の化学反応の例で使ったものと同じ微分方程式を使っています。

関連情報

今回はこちらの講座向けにつくった例題のうち、講座で使わなかったものを公開しています↓

こちらでは、微分方程式を組み込んだ Google のモデルの解説をしています↓