NumPyro による微分方程式のパラメータ推定 – SIR model
概要
コロナの流行などもあり、すっかり有名になった SIR モデルですが、このモデルのパラメータ推定を NumPyro でやってみました。なお、NumPyro は基本的には Windows では動きませんので(Jax が対応していないため)、Windows の方は Google Colab 等でお試し頂けたらと思います。
Install Packages
まず、NumPyro を使うための準備として、パッケージのインストールを行います。Google Colab などの場合はこのまま使って頂いてよいと思うのですが、仮想環境などを作っている場合は環境が壊れてしまわないようにご注意下さい。
NumPyro は JAX に依存しているため、JAX のバージョンによってはうまく動かないことがあります。下のコマンドは JAX が GPU でも動くようにしているので、少し複雑になっていますが、CPUだけでよければもうちょっと簡単になります。現時点(2021.9.30)で最新である version 0.2.21 の JAX と NumPyro とはどうも相性が悪そうなので、ご注意下さい。少し古めの JAX がお勧めです。
また、Google Colab の場合はデフォルトで JAX が入っていますので、ランタイムの再起動もお忘れなく!
!pip install --upgrade jax==0.2.17 jaxlib==0.1.71+cuda111 -f https://storage.googleapis.com/jax-releases/jax_releases.html
!pip install numpyro==0.7.2
!pip install arviz==0.11.2
!pip install japanize_matplotlib
Import Packages
JAX と NumPyro などのパッケージをインポートしていきます。
import jax
import jax.numpy as jnp
import jax.experimental.ode as ode
import numpyro
import numpyro.distributions as dist
import arviz as az
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
plt.rcParams['font.size'] = 12
NumPyro の実行環境を設定します。もし GPU が使いたい場合は、下の set_platform のところで、’gpu’ を設定して下さい。しかし、なぜか GPU に設定すると、CPU より遅くなります(なぜだろう…)。
numpyro.set_platform('cpu')
numpyro.set_host_device_count(4)
Generate Data
今回あてはめるデータは本物のデータではなく、小さな村でインフルエンザみたいな感染症の流行があったというような状況を想定して、シミュレーションで生成してみます。
この感染症のモデル化に使うのは、次のような基本的な SIR モデルですが、簡単のため免疫保持者(Recovered) にあたる R の部分のダイナミクスに関する式は省いています。
$$ \begin{align} \frac{dS}{dt} &= -\beta SI\\ \frac{dI}{dt} &= \beta SI – \gamma I\\ \end{align} $$
SIR モデルについては、さまざまなブログ等でも紹介がありますが、とりあえず Wikipedia などを見て頂くとよいかもしれません。
まずは、この SIR モデルを関数で表現して、実際に解いてみます。
def dz_dt(z, t, beta, gamma):
S = z[0]
I = z[1]
dS_dt = -beta * S * I
dI_dt = beta * S * I - gamma * I
return jnp.stack([dS_dt, dI_dt])
beta = 1.0
gamma = 0.25
t = jnp.arange(20).astype(float)
z = ode.odeint(dz_dt, [0.99, 0.01], t, beta, gamma, rtol=1e-8)
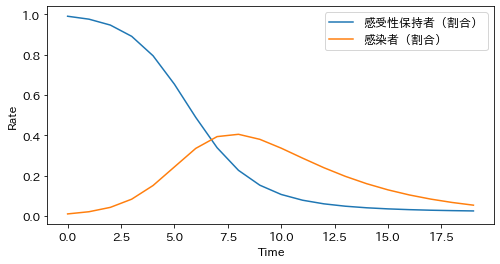
微分方程式の初期値としては、S の感受性保持者(Susceptible)と I の感染者(Infected)の比率をそれぞれ 99% と 1% にしています。この微分方程式の解をプロットすると、以下のような感じになります。
S = z[0]
I = z[1]
fig = plt.figure(figsize=(8, 4))
plt.plot(t, S, color='C0', label='感受性保持者(割合)')
plt.plot(t, I, color='C1', label='感染者(割合)')
plt.xlabel('Time')
plt.ylabel('Rate')
plt.legend();
次に、この微分方程式の解からデータを捏造します。村で 1% ほどの感染者が出た時点から8日間の間、毎日感染者数が記録できているものとして、データをつくります。村における感染者は、村での潜在的な感染者の割合(Infected)に従って、観測されるという仮定を置きます。感染者の割合(Infected)に、村の人口(1000人)をかけた値を平均とするポアソン分布に従って感染者が発生するものとします。
num_people = 1000
num_data = 8
t_observed = t[:num_data]
I_observed = np.random.poisson(I[:num_data] * num_people)
fig = plt.figure(figsize=(8, 4))
plt.plot(t_observed, I_observed, 'o', color='C2', label='観測データ')
plt.plot(t, S * num_people, '--', color='C0', label='感受性保持者数')
plt.plot(t, I * num_people, '--', color='C1', label='感染者数')
plt.xlabel('Time')
plt.ylabel('Number')
plt.legend();
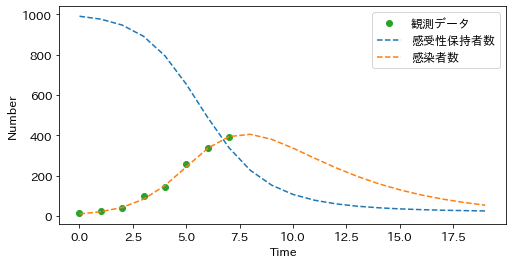
以上のようにして、8日間の感染者数のデータを捏造することができました。
Define Model & Inference
では、今度は逆に観測データから微分方程式のパラメータを推定してみることにします。データをシミュレーションで生成したときには、感染率(beta)と回復率(gamma)がわかっているものとして計算を行いましたが、今度はこれらのパラメータが未知であるとして、データから逆に求められるかを考えてみます。つまり、逆問題を考えます。
NumPyro の場合、モデルは関数として定めていきます。パラメータに事前分布を置いて、順方向でデータが観測されるまでのプロセスを関数に記述していきます。
def model(num_people, t, y=None):
# 感受性保持者(S)と感染者(I)の初期値に関する事前分布
S_init = numpyro.sample('S_init', dist.Beta(1, 1))
I_init = numpyro.deterministic('I_init', 1 - S_init)
z_init = jnp.array([S_init, I_init])
# 感染率(beta)と回復率(gamma)に関する事前分布
beta = numpyro.sample('beta', dist.HalfNormal(5))
gamma = numpyro.sample('gamma', dist.HalfNormal(5))
# 微分方程式のソルバー
z = ode.odeint(dz_dt, z_init, t, beta, gamma, rtol=1e-6, atol=1e-5, mxstep=1000)
# 観測データからの尤度の計算
numpyro.sample('y', dist.Poisson(z[:, 1] * num_people), obs=y)
次に、マルコフ連鎖モンテカルロ法(MCMC)と呼ばれる方法で、パラメータを逆に推定していきます。つまり、上でパラメータに事前確率分布を置いたモデルを設定することができたので、今度はデータを元にパラメータの事後確率分布を求めます(ベイズ推定)。
本当は、この事後確率分布を直接数式として計算できるとよいのですが、今回のモデルでは難しいので、マルコフ連鎖モンテカルロ法(MCMC)と呼ばれる方法を使います。マルコフ連鎖モンテカルロ法(MCMC)は、事後確率分布から大量のサンプルを発生させるための手法のひとつで、これらのサンプルたちを使うことで、事後確率分布に関するさまざまな情報を調べることができるようになります。
%%time
nuts = numpyro.infer.NUTS(model)
mcmc = numpyro.infer.MCMC(nuts, num_warmup=1000, num_samples=3000, num_chains=4, progress_bar=False)
mcmc.run(jax.random.PRNGKey(0), num_people, t_observed, y=I_observed)
trace = mcmc.get_samples()
CPU times: user 13.1 s, sys: 27.1 ms, total: 13.2 s
Wall time: 9.39 s事後確率分布からのサンプルは既に取れているのですが、Arviz による事後解析のために Arviz の InferenceData オブジェクトへの変換を行っておきます。
idata = az.from_numpyro(mcmc)
az.plot_trace(idata);

az.summary(idata)
| mean | sd | hdi_3% | hdi_97% | mcse_mean | mcse_sd | ess_bulk | ess_tail | r_hat | |
|---|---|---|---|---|---|---|---|---|---|
| I_init | 0.012 | 0.002 | 0.009 | 0.015 | 0.000 | 0.000 | 2284.0 | 3018.0 | 1.0 |
| S_init | 0.988 | 0.002 | 0.985 | 0.991 | 0.000 | 0.000 | 2284.0 | 3018.0 | 1.0 |
| beta | 0.944 | 0.085 | 0.778 | 1.099 | 0.002 | 0.001 | 2051.0 | 2449.0 | 1.0 |
| gamma | 0.228 | 0.042 | 0.150 | 0.307 | 0.001 | 0.001 | 2243.0 | 2534.0 | 1.0 |
fig, axes = plt.subplots(2, 2, figsize=(10, 8))
az.plot_posterior(idata, ax=axes);
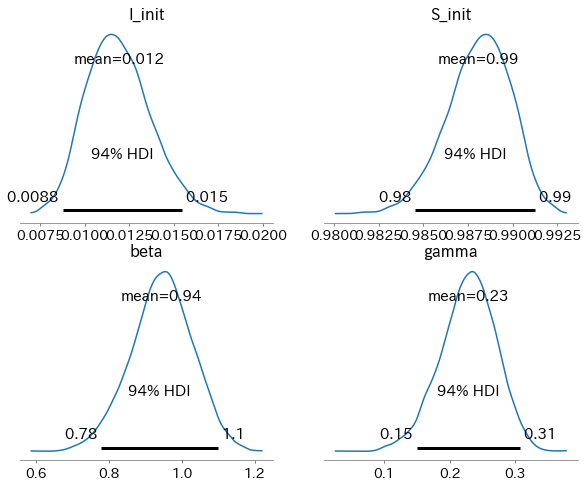
Check Prediction
ここまでの計算によりパラメータの事後確率分布がわかったので、次に未来がどうなるかを微分方程式により予測してみます。データが観測された8日間を含む30日の期間で予測を行ってみます。この微分方程式の場合、その解は初期値を決めればほぼ一意的に決まりそうですが、微分方程式のパラメータの予測に広がり(分布)があるので、予測にも広がり(分布)があります。この分布は「事後予測分布」と呼ばれます。
t_pred = jnp.arange(30).astype(float)
predictive = numpyro.infer.Predictive(model, trace)
ppc_samples = predictive(jax.random.PRNGKey(2), num_people, t_pred)
y_pred = ppc_samples['y']
mu_pred = jnp.mean(y_pred, 0)
pi_pred = jnp.percentile(y_pred, (5, 95), 0)
plt.figure(figsize=(9, 5))
plt.plot(t_observed, I_observed, 'o', color='C2', label='感染者数(観測値)')
plt.plot(t_pred, mu_pred, '-.', color='C1', label="感染者数(予測値)")
plt.fill_between(t_pred, pi_pred[0, :], pi_pred[1, :], color='C1', alpha=0.2)
plt.title('事後予測分布(90%-Bayesian Prediction Interval)')
plt.xlabel('Time')
plt.ylabel('Number')
plt.legend();
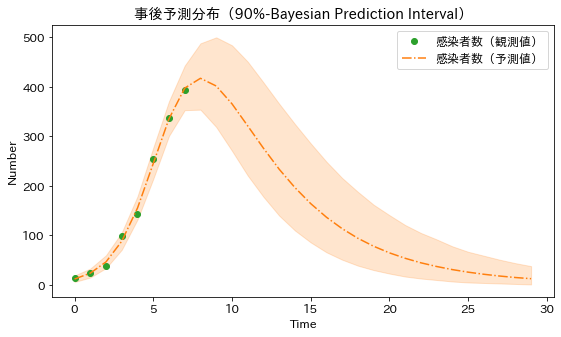
このグラフでは、この事後予測分布の両端を 5% ずつ切ったベイズ予測区間(※)を表示しています。
※ なお、用語の使い方に関しては、松浦先生の「StanとRでベイズ統計モデリング」(いわゆるアヒル本)の 2.5章「ベイズ信頼区間とベイズ予測区間」を参考にしています。
Summary
通常、こういったデータで単純な時系列のモデルで未来予測をしてしまうと、どこまでも感染者が増えて行ってしまうような線形な予測をしてしまったり、村の人口の上限である 1000人の近くでサチる、みたいな予測をしてしまいそうですが、モデルに微分方程式のようなメカニズムを入れ込むことで、より現実的な予測ができていることがわかります。
ちなみに、今回ご紹介したモデルは、下の論文の 2.4章 “Deterministic ODE-based models" で紹介されている
モデルを参考に作りました。Appendix B. “Stan model code and implementation"(P28-29)のところに Stan のコードがあります。
https://arxiv.org/pdf/1903.00423.pdf
PyMC3 でも SIRモデルが紹介されている例題があります。SIRモデルは、Lotka-Volterra モデルなどと並んでよく紹介されているようです。
微分方程式でのパラメータ推定の問題については、Bob Carpenter さんの記事が非常に参考になりました。こちらは Lotka-Volterra モデルについての記事ですが、面白い記事なのでぜひ。



