情報量基準による微分方程式のモデル選択
概要
前回の記事と同じく、今回も化学反応に関する微分方程式を扱いたいと思います。詳細は前回の記事をご覧下さい。
微分方程式もデータも全く同じものですが、解析の方向性を少しだけ変えます。
前回は下のような反応速度式に含まれる速度定数(k)と次数(m, n)の両方をデータから一気に推定してしまっていたのですが、今回は次数(m, n)は固定して、速度定数(k)のみを推定することにします。
更に、背景の知識から「m=1, n=1 か、m=2, n=1 のいずれかのパターンになることはわかっているものの、どちらが正しいのか決め兼ねている」…そんな状況を考えてみます(そんな状況が本当にあるかはともかく…)。
こういった種類の問題は統計モデリングの世界では、「モデル選択」の問題として知られている問題ですが、このモデル選択の問題を情報量基準(WAIC)を使って考えてみることにします。
Install Packages
まずは、NumPyro をインストールします。Google Colab なら下のコマンドでうまく行くはずですが、自前の環境でされている方は環境を壊さないようにご注意下さい。また、Google Colab をお使いの方はランタイムの再起動をお忘れなく!
!pip install --upgrade jax==0.2.17 jaxlib==0.1.71+cuda111 -f https://storage.googleapis.com/jax-releases/jax_releases.html
!pip install numpyro==0.7.2
!pip install arviz==0.11.2
!pip install japanize_matplotlib
Import Packages
必要なパッケージをインポートします。
import jax
import jax.numpy as jnp
import jax.experimental.ode as ode
import numpyro
import numpyro.distributions as dist
import arviz as az
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
import seaborn as sns
import japanize_matplotlib
plt.rcParams['font.size'] = 14
numpyro.set_platform('cpu')
numpyro.set_host_device_count(4)
Generate Data
この部分の処理は完全に前回と同じものです。微分方程式の解を計算して、そこに雑音を加えることで、測定データを捏造します。
def dz_dt(z, t, k, m, n):
A = z[0]
B = z[1]
C = z[2]
V = k * jnp.power(A, m) * jnp.power(B, n) # 反応速度
dA_dt = -2.0 * V
dB_dt = -V
dC_dt = 2.0 * V
return jnp.stack([dA_dt, dB_dt, dC_dt])
m_true = 2.0 # 次数(A)
n_true = 1.0 # 次数(B)
k_true = 0.2 # 速度定数
t_true = jnp.arange(0, 20).astype(float)
z_init = jnp.array([1.4, 1.0, 0.1]).astype(float) # 濃度の初期値
z_true = ode.odeint(dz_dt, z_init, t_true, k_true, m_true, n_true)
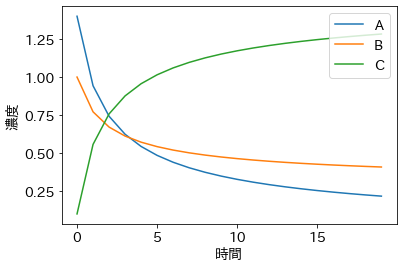
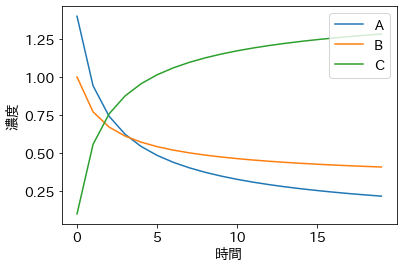
plt.plot(z_true, label=['A', 'B', 'C'])
plt.xlabel('時間')
plt.ylabel('濃度')
plt.legend(loc='upper right');
t_observed = t_true
z_observed = np.random.lognormal(mean=np.log(z_true), sigma=0.05)
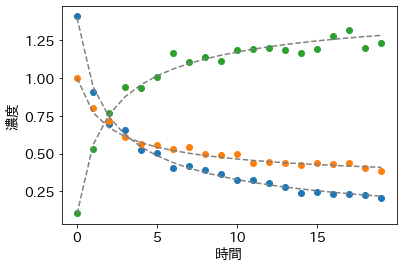
plt.plot(z_observed, 'o')
plt.plot(z_true, '--', color='gray')
plt.xlabel('時間')
plt.ylabel('濃度');
Define Model & Inference (Model-A)
まずは、m=2, n=1 とした場合のモデルに対して、データをあてはめてみます。
def model_A(t, z_observed=None):
m = 2.0
n = 1.0
A_init = numpyro.sample('A_init', dist.HalfNormal(10))
B_init = numpyro.sample('B_init', dist.HalfNormal(10))
C_init = numpyro.sample('C_init', dist.HalfNormal(10))
k = numpyro.sample('k', dist.HalfNormal(10))
z_init = jnp.stack([A_init, B_init, C_init])
z_mean = ode.odeint(dz_dt, z_init, t, k, m, n)
sigma = numpyro.sample('sigma', dist.HalfNormal(10))
numpyro.sample('y', dist.LogNormal(jnp.log(z_mean), sigma), obs=z_observed)
今回のモデルでは、チェインによっては MCMC がうまく収束してくれないことがあったため、MCMC に初期値を設定しています。
init_values = {'k':0.2,'A_init':1.4,'B_init':1.0,'C_init':0.1,'sigma':0.05}
nuts = numpyro.infer.NUTS(model_A)
mcmc = numpyro.infer.MCMC(nuts, num_warmup=1000, num_samples=1000, num_chains=4, progress_bar=False)
mcmc.run(jax.random.PRNGKey(0), t_observed, z_observed=z_observed)
idata_A = az.from_numpyro(mcmc)
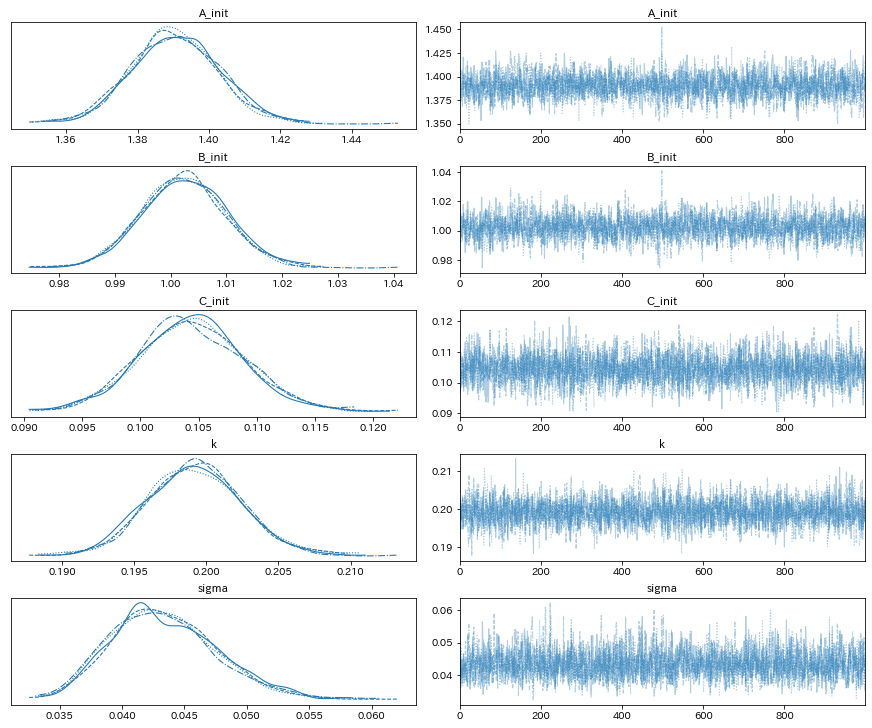
az.plot_trace(idata_A);
az.summary(idata_A)
| mean | sd | hdi_3% | hdi_97% | mcse_mean | mcse_sd | ess_bulk | ess_tail | r_hat | |
|---|---|---|---|---|---|---|---|---|---|
| A_init | 1.390 | 0.012 | 1.368 | 1.414 | 0.0 | 0.0 | 2267.0 | 2507.0 | 1.0 |
| B_init | 1.002 | 0.008 | 0.988 | 1.016 | 0.0 | 0.0 | 2342.0 | 2651.0 | 1.0 |
| C_init | 0.104 | 0.005 | 0.095 | 0.113 | 0.0 | 0.0 | 2807.0 | 2699.0 | 1.0 |
| k | 0.199 | 0.003 | 0.193 | 0.206 | 0.0 | 0.0 | 3247.0 | 2434.0 | 1.0 |
| sigma | 0.043 | 0.004 | 0.036 | 0.051 | 0.0 | 0.0 | 2913.0 | 2595.0 | 1.0 |
微分方程式の初期値と反応定数を概ね正しく推定できているようです。
Define Model & Inference (Model-B)
次に、m=1, n=1 とした場合のモデルに対して、データをあてはめてみます。
def model_B(t, z_observed=None):
m = 1.0
n = 1.0
A_init = numpyro.sample('A_init', dist.HalfNormal(10))
B_init = numpyro.sample('B_init', dist.HalfNormal(10))
C_init = numpyro.sample('C_init', dist.HalfNormal(10))
k = numpyro.sample('k', dist.HalfNormal(10))
z_init = jnp.stack([A_init, B_init, C_init])
z_mean = ode.odeint(dz_dt, z_init, t, k, m, n)
sigma = numpyro.sample('sigma', dist.HalfNormal(10))
numpyro.sample('y', dist.LogNormal(jnp.log(z_mean), sigma), obs=z_observed)
init_values = {'k':0.2,'A_init':1.4,'B_init':1.0,'C_init':0.1,'sigma':0.5}
init_strategy = numpyro.infer.init_to_value(values=init_values)
nuts = numpyro.infer.NUTS(model_B, init_strategy=init_strategy)
mcmc = numpyro.infer.MCMC(nuts, num_warmup=1000, num_samples=1000, num_chains=4, progress_bar=False)
mcmc.run(jax.random.PRNGKey(0), t_observed, z_observed=z_observed)
idata_B = az.from_numpyro(mcmc)
az.plot_trace(idata_B);
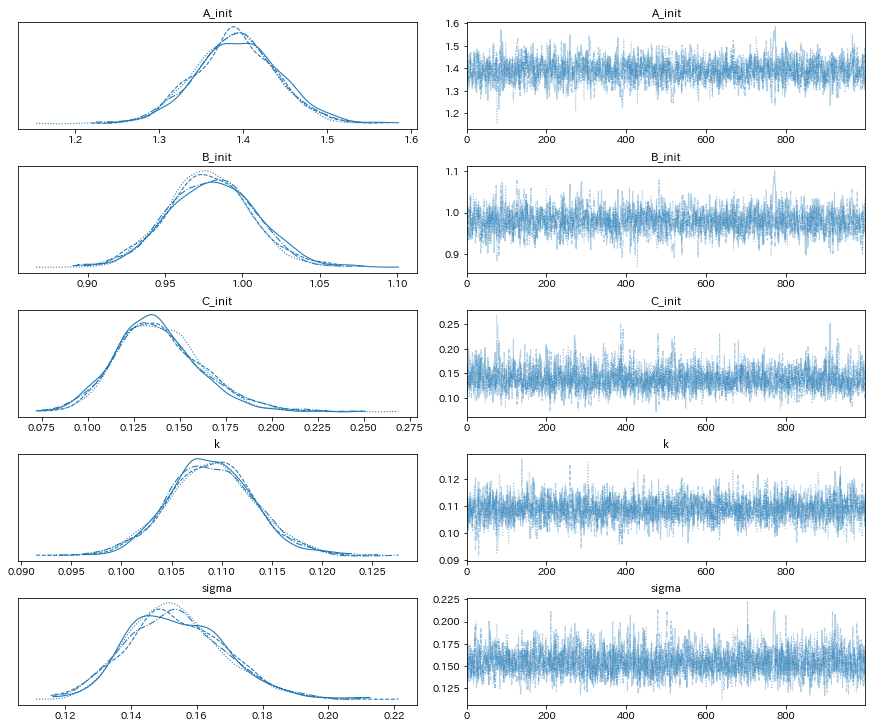
az.summary(idata_B)
| mean | sd | hdi_3% | hdi_97% | mcse_mean | mcse_sd | ess_bulk | ess_tail | r_hat | |
|---|---|---|---|---|---|---|---|---|---|
| A_init | 1.391 | 0.049 | 1.298 | 1.482 | 0.001 | 0.001 | 1585.0 | 1946.0 | 1.0 |
| B_init | 0.979 | 0.028 | 0.928 | 1.034 | 0.001 | 0.000 | 1623.0 | 1794.0 | 1.0 |
| C_init | 0.139 | 0.023 | 0.097 | 0.182 | 0.001 | 0.000 | 2035.0 | 2266.0 | 1.0 |
| k | 0.109 | 0.004 | 0.100 | 0.117 | 0.000 | 0.000 | 2679.0 | 2331.0 | 1.0 |
| sigma | 0.154 | 0.015 | 0.126 | 0.181 | 0.000 | 0.000 | 2486.0 | 2288.0 | 1.0 |
微分方程式の初期値は先のモデルと同じように概ね正しく推定できていますが、速度定数は先のモデルから推定された値とは異なっています。
Compare Models
次に、このようにパラメータ推定を行ったモデルたちの情報量基準(WAIC)を調べてみます。WAIC は、東京工業大学の渡辺澄夫先生により考案された非常に汎用性の高い情報量基準であり、渡辺先生のお言葉によれば「WAIC は統計学の知識がない人でも誰でも使うことができます」とのことなので、無邪気に今回のモデルにも使ってみることにします。
WAIC は arviz と呼ばれるパッケージに関数として含まれているので、この関数を使って2つのモデルの WAIC を計算してみます。
az.waic(idata_A, scale='deviance')
Computed from 4000 by 60 log-likelihood matrix
Estimate SE
deviance_waic -269.18 12.58
p_waic 4.25 -
There has been a warning during the calculation. Please check the results.
az.waic(idata_B, scale='deviance')
Computed from 4000 by 60 log-likelihood matrix
Estimate SE
deviance_waic -110.57 14.16
p_waic 8.71 -
There has been a warning during the calculation. Please check the results.
WAIC は deviance をスケールに取った場合には、小さい方がよいモデルということになるので、今回の場合は Model-A の方が Model-B よりもよいモデルだったということがわかります。
次に、これらの情報量基準を比較しやすいようにまとめたものを表示してみます。
dict_idata = {'Model-A':idata_A, 'Model-B':idata_B}
df_waic = az.compare(dict_idata, ic='waic', scale='deviance')
df_waic
/home/ohta/anaconda3/envs/numpyro-test/lib/python3.9/site-packages/arviz/stats/stats.py:145: UserWarning: The default method used to estimate the weights for each model,has changed from BB-pseudo-BMA to stacking
warnings.warn(
/home/ohta/anaconda3/envs/numpyro-test/lib/python3.9/site-packages/arviz/stats/stats.py:1405: UserWarning: For one or more samples the posterior variance of the log predictive densities exceeds 0.4. This could be indication of WAIC starting to fail.
See http://arxiv.org/abs/1507.04544 for details
warnings.warn(
/home/ohta/anaconda3/envs/numpyro-test/lib/python3.9/site-packages/arviz/stats/stats.py:1405: UserWarning: For one or more samples the posterior variance of the log predictive densities exceeds 0.4. This could be indication of WAIC starting to fail.
See http://arxiv.org/abs/1507.04544 for details
warnings.warn(
| rank | waic | p_waic | d_waic | weight | se | dse | warning | waic_scale | |
|---|---|---|---|---|---|---|---|---|---|
| Model-A | 0 | -269.182979 | 4.248271 | 0.000000 | 1.0 | 12.580428 | 0.000000 | True | deviance |
| Model-B | 1 | -110.573733 | 8.707120 | 158.609246 | 0.0 | 14.160264 | 15.708873 | True | deviance |
計算過程でたくさん warning が出てしまっていますが、これは「もしかしたら計算結果はあまり信用できんかもしれんよ」という感じの warning なので、とりあえずスルーしてしまいます。
上の DataFrame では rank というところが、モデルを良い順に並べたときの順位になっています。更に、計算された情報量基準をグラフとして可視化してやると、次のようになります。
az.plot_compare(df_waic, figsize=(8, 3));
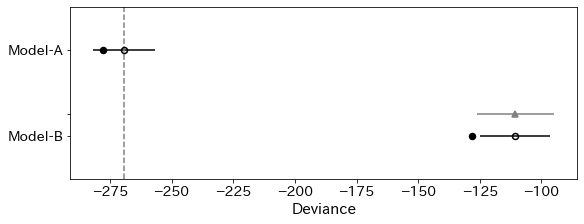
Model-A を表す白丸が Model-B の白丸よりずっと左にありますが、左にある方が値が小さいことになりますので、Model-A の方がよいということになります。
Summary
統計モデリングではよく回帰モデルなどで、こうした情報量基準を使ったモデル選択を行いますが、今回は微分方程式を含むモデルに対して、こうしたモデル選択ができるかの実験を行ってみました。
渡辺先生のサイトには「微分方程式を含むモデルでも大丈夫!」とは明示的には書かれていないので、ちょっと心配な部分もあるのですが、もっとやばそうなモデルでも大丈夫そうなので、今回は気楽に使ってみてしまっています。
化学の知識がほとんどないので、まるでトンチンカンなことを言っている可能性もあるのですが、使えそうな部分がありましたら、ぜひ研究等のお役に立てて頂けたら幸いです。