NumPyro による微分方程式のパラメータ推定 – バネマス系
概要
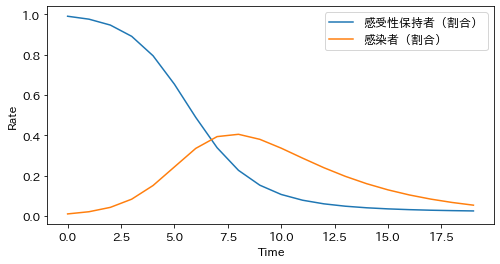
前回ご紹介した感染症のモデル(SIR-model)に引き続いて、今回はバネマスダンパ系と呼ばれる運動方程式において、前回と同じく微分方程式のパラメータ推定をやってみたいと思います。
機械を相手にする場合、測定データは一定のサンプリング間隔で取れることが多いので、微分方程式は離散化してしまい、普通に状態空間モデルとして扱った方が便利なことは多いのですが、測定データが必ずしも等間隔には取れないとか、そういうケースでは有効に使えるケースもあるのではないかと思い、紹介してみることにしました。
Mass-Spring-Dumper System
バネマスダンパ系は、制御工学で非常によく出てくる例題で、ポンチ絵を書くとこんな感じになります。
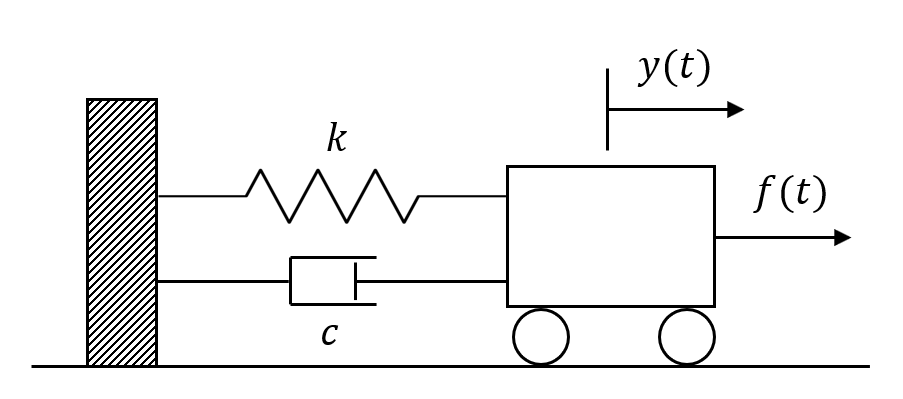
基本的に質点(Mass)とバネ(Spring)と減衰器(Dumper)を結びつけたシステムで、一番イメージしやすいのが自動車のサスペンションではないかと思いますが、このバネと減衰器の組み合わせ次第で、自動車の乗り心地が大きく変化します(おそらく現代の自動車は私が想像しているよりももっと複雑だとは思いますが…)。
このバネマスダンパ系と呼ばれる微分方程式は、式で書くと次のような感じになります。
$$ \begin{equation} m \ddot{y}(t) + c \dot{y}(t) + k y(t) = f(t) \end{equation} $$
c は減衰器の係数で減衰係数と呼ばれます。k はバネ定数です。これらの定数がわからないものとして、データからこれらの定数を推定する、というのが、これからやろうとしていることになります。
Install Packages
NumPyro は JAX のバージョンに多少敏感なので、ちょっと古めの JAX を選んでパッケージをインストールします。また、Google Colab の場合はデフォルトで JAX が入っていますので、ランタイムの再起動もお忘れなく!
!pip install --upgrade jax==0.2.17 jaxlib==0.1.71+cuda111 -f https://storage.googleapis.com/jax-releases/jax_releases.html
!pip install numpyro==0.7.2
!pip install arviz==0.11.2
!pip install japanize_matplotlib
Import Packages
JAX と NumPyro などのパッケージをインポートしていきます。
import jax
import jax.numpy as jnp
import jax.experimental.ode as ode
import numpyro
import numpyro.distributions as dist
import arviz as az
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
plt.rcParams['font.size'] = 14
numpyro.set_platform('cpu')
numpyro.set_host_device_count(4)
Generate Data
今回もシミュレーションでデータを生成していきます。また、微分方程式はそのままだと odeint に解かせてやることができないので、次のようにバラしておきます。
$$ \begin{align} \dot{y}(t) &= v(t)\\ \dot{v}(t) &= -k y(t) – c \dot{v(t)} + f(t)\\ \end{align} $$
質点の速度と変位は最初ゼロにセットしますが、最初の2秒間だけ 1 [N] の力で引いてやることにします。但し、外力は次のような感じで式でかけるものないと、うまく微分方程式に入力してやることができないので、制御系の解析などに使うにはちょっと実用的ではないかもしれないです…
def f(t, F=1):
return jnp.where(t < 2, F, 0)
def dz_dt(z, t, m, c, k):
y = z[0]
v = z[1]
dy_dt = v
dv_dt = (- k * y - c * v + f(t)) / m
return jnp.stack([dy_dt, dv_dt])
m = 1.0 # 質量
c = 1.0 # 減衰係数
k = 1.0 # バネ定数
t_true = jnp.arange(0, 10, 0.1).astype(float)
z_init = jnp.array([0, 0]).astype(float)
z = ode.odeint(dz_dt, z_init, t_true, m, c, k)
y_true = z[:, 0]
v_true = z[:, 1]
plt.plot(t_true, y_true)
plt.title('Mass-Spring-Dumper System')
plt.xlabel('時間 [s]')
plt.ylabel('変位 [m]');
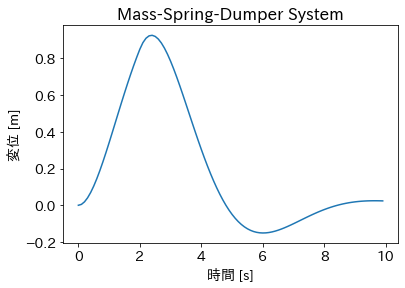
最初の2秒間だけプラスの方向に変位が起こり、次に元の方向へ戻ろうとしている動きがわかります。この微分方程式の解に少しだけ雑音を加えて、測定データを捏造します。
np.random.seed(0)
t_observed = t_true[::5]
y_observed = np.random.normal(y_true[::5], 0.05)
plt.plot(t_true, y_true)
plt.plot(t_observed, y_observed, 'o')
plt.title('Mass-Spring-Dumper System')
plt.xlabel('時間 [s]')
plt.ylabel('変位 [m]');
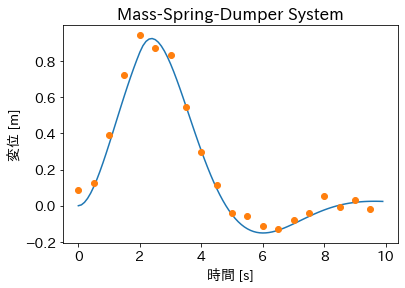
以上のようにして、バネマス系の測定データを捏造することができました。
Define Model & Inference
次に、この観測データから微分方程式のパラメータを推定してみることにします。データをシミュレーションで生成したときには、減衰係数(c)とバネ定数(k)がわかっているものとして計算を行いましたが、今度はこれらのパラメータが未知であるとして、データから逆に求められるかを考えてみます。つまり、逆問題を考えます。
NumPyro の場合、モデルは関数として定めていきます。パラメータに事前分布を置いて、順方向でデータが観測されるまでのプロセスを関数に記述していきます。
def model(t, y_observed=None):
# 変位(y)と速度(v)の初期値に関する事前分布
y_init = numpyro.sample('y_init', dist.Normal(0, 10))
v_init = numpyro.sample('v_init', dist.Normal(0, 10))
z_init = jnp.stack([y_init, v_init])
# 減衰係数(c)とバネ定数(k)に関する事前分布
c = numpyro.sample('c', dist.HalfNormal(10))
k = numpyro.sample('k', dist.HalfNormal(10))
# 微分方程式のソルバー
z = ode.odeint(dz_dt, z_init, t, m, c, k)
# 観測データからの尤度の計算
sd_y = numpyro.sample('sigma', dist.HalfNormal(10))
numpyro.sample('y', dist.Normal(z[:, 0], sd_y), obs=y_observed)
次に、マルコフ連鎖モンテカルロ法(MCMC)と呼ばれる方法で、パラメータを逆に推定していきます。つまり、上でパラメータに事前確率分布を置いたモデルを設定することができたので、今度はデータを元にパラメータの事後確率分布を求めます(ベイズ推定)。
本当は、この事後確率分布を直接数式として計算できるとよいのですが、今回のモデルでは難しいので、マルコフ連鎖モンテカルロ法(MCMC)と呼ばれる方法を使います。マルコフ連鎖モンテカルロ法(MCMC)は、事後確率分布から大量のサンプルを発生させるための手法のひとつで、これらのサンプルたちを使うことで、事後確率分布に関するさまざまな情報を調べることができるようになります。
%%time
nuts = numpyro.infer.NUTS(model, target_accept_prob=0.95)
mcmc = numpyro.infer.MCMC(nuts, num_warmup=2000, num_samples=1000, num_chains=4, progress_bar=False)
mcmc.run(jax.random.PRNGKey(0), t_observed, y_observed=y_observed)
mcmc_samples = mcmc.get_samples()
idata = az.from_numpyro(mcmc)
CPU times: user 19.2 s, sys: 44 ms, total: 19.3 s
Wall time: 13.3 s
az.plot_trace(idata);
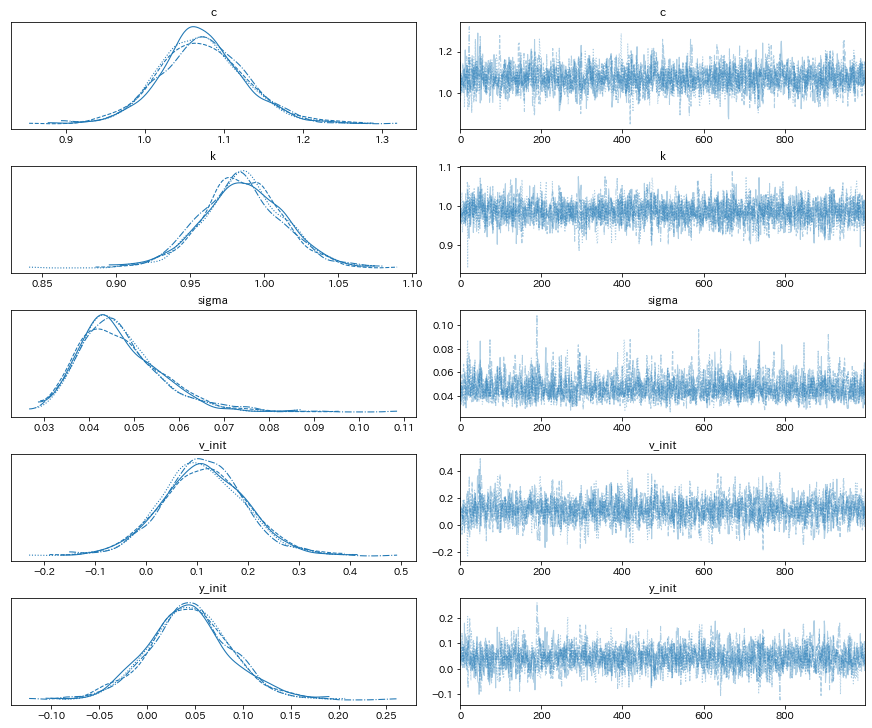
az.summary(idata)
| mean | sd | hdi_3% | hdi_97% | mcse_mean | mcse_sd | ess_bulk | ess_tail | r_hat | |
|---|---|---|---|---|---|---|---|---|---|
| c | 1.072 | 0.055 | 0.970 | 1.176 | 0.001 | 0.001 | 2083.0 | 2204.0 | 1.0 |
| k | 0.985 | 0.028 | 0.934 | 1.040 | 0.001 | 0.000 | 2141.0 | 2420.0 | 1.0 |
| sigma | 0.047 | 0.009 | 0.032 | 0.064 | 0.000 | 0.000 | 1898.0 | 2058.0 | 1.0 |
| v_init | 0.113 | 0.084 | -0.042 | 0.273 | 0.002 | 0.002 | 1488.0 | 2107.0 | 1.0 |
| y_init | 0.045 | 0.044 | -0.038 | 0.127 | 0.001 | 0.001 | 1591.0 | 1771.0 | 1.0 |
fig, axes = plt.subplots(2, 2, figsize=(10, 8))
az.plot_posterior(idata, var_names=['y_init', 'v_init', 'c', 'k'], ax=axes)
fig.subplots_adjust(hspace=0.4)
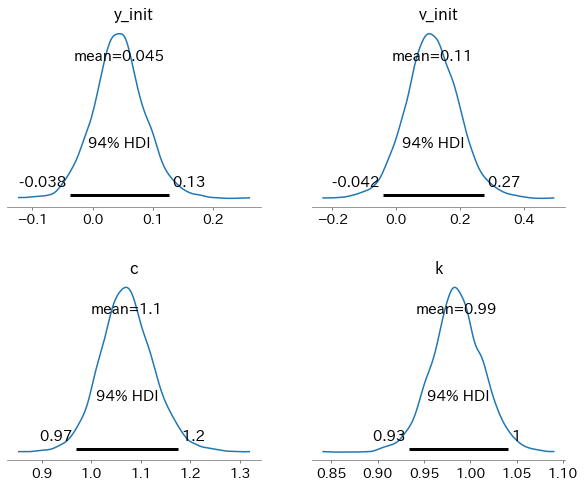
Check Prediction
ここまでの計算によりパラメータの事後確率分布がわかったので、次に実験を行ったときにどれくらい測定値がバラつくかを微分方程式により予測してみます。この微分方程式の場合、その解は初期値を決めればほぼ一意的に決まりそうですが、観測時の雑音等があるため、測定値の予測には広がりがあります。また、推定した微分方程式のパラメータも広がり(分布)があるので、それによっても予測は広がりを持つことになります。
t_pred = jnp.arange(0, 10, 0.1).astype(float)
predictive = numpyro.infer.Predictive(model, mcmc_samples)
ppc_samples = predictive(jax.random.PRNGKey(2), t_pred)
y_pred = ppc_samples['y']
mu_pred = jnp.mean(y_pred, 0)
pi_pred = jnp.percentile(y_pred, (5, 95), 0)
plt.figure(figsize=(8, 6))
plt.plot(t_observed, y_observed, 'o', color='C1', label='観測値')
plt.plot(t_true, y_true, '--', color='C2', label='真値')
plt.plot(t_pred, mu_pred, '-.', color='C0', label='予測値 (平均)')
plt.fill_between(t_pred, pi_pred[0, :], pi_pred[1, :], color='C0', alpha=0.2)
plt.title('事後予測分布')
plt.xlabel('時間 [s]')
plt.ylabel('変位 [m]')
plt.legend();
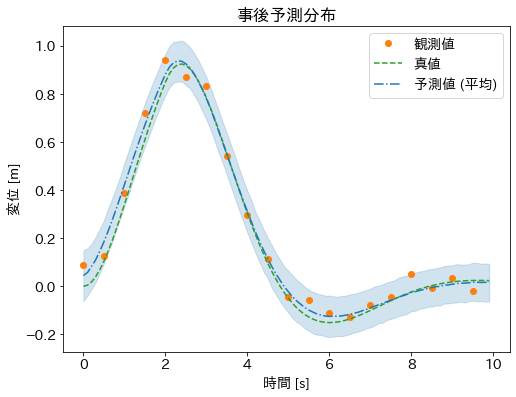
このグラフでは薄青の帯によって、事後予測分布の両端を 5% ずつ切ったベイズ予測区間(※)を表示していますが、実際の測定データもほぼこの帯の中に収まっていることがわかります。
※ なお、用語の使い方に関しては、松浦先生の「StanとRでベイズ統計モデリング」(いわゆるアヒル本)の 2.5章「ベイズ信頼区間とベイズ予測区間」を参考にしています。
Summary
今回、制御等でよく使われるバネマスダンパ系の微分方程式で、測定データから微分方程式のパラメータを推定してみました。前回は、感染症のモデル(SIR-model)のパラメータ推定をやってみましたが、どちらのモデルでも比較的に簡単な手順で割と高速にパラメータが推定できることが見て頂けたのではないかと思います。
NumPyro は Windows 上では動かすのが難しいと思いますが、Google Colab などであれば簡単に動かすことができますので、ぜひお試し頂けたらと思います。