需要予測と利益の最大化
機械学習を使った予測では、一般的に「精度さえ出ればいい」という思考パターンにハマってしまいがちだけれどれも、本当にそれで大丈夫なのかな?ということを最近よく考える。予測精度さえよければ、本当に顧客の要望は叶えられるのか?
この記事では、アルゴリズムによる需要予測と顧客の要望のズレについて、簡単な例を挙げて説明をしてみたいと思う。
とある街のうどん店の話
とある街に小さなうどん店があり、あなたがその店の店主だとする。あなたは毎日店でどれくらいのうどんが売れるのかを予想して、仕入れや仕込みをしないといけないが、予想はなかなか当たらない。
そこで、あなたはある IT 企業に相談して、AI に基づく需要予測のソフトウェアを導入することにした。このソフトウェアでは数十もの最先端のアルゴリズムにより需要予測を行い、その中で最も性能のよいアルゴリズムを選択することにより、非常に精度の高い予測を行えるのだという。そこであなたはさっそくこのソフトウェアを導入し、需要予測をしてみることにした。
ソフトウェアは過去のデータを元に、気温や湿度、曜日などのデータを利用してその日の需要を予測するのだという。導入初日、店主はさっそく今日の気温や湿度、曜日等のデータを入力して需要を予測してみることにした。
導入初日、ソフトウェアの予測したうどんの販売個数は 30杯。店主は、このソフトウェアの予測通り 30杯分のうどんを仕込んで置いたが、結局うどんは予想よりも早く売り切れてしまい、いつもよりも早く店を閉めることになってしまった。本当だったら、40杯くらいは行けたかもしれないような印象だった。
次の日、同じようにソフトウェアに販売個数を予測させてみると、ソフトウェアは再び 30杯の販売個数を予測している。しかし、昨日は大分早く売り切れてしまったので、今度は AI をあまり信用せずに、少しだけ多めに 35杯分のうどんの仕込みをしておくことにする。結局、その日は 32杯のうどんが売れたので、AI を信用し過ぎなくて大正解!だったのだが、もしかしたらたまたまだったのかもしれない。
うどんの価格は 350円で、原価は 50円ほどなので、AI の予測より多めに仕込んでおくことで、600円ほど得をしたことになる。
次の日、またソフトウェアに販売個数を予測させてみると、再び 30杯の販売個数を予測した。「こいつ壊れてんじゃねーの?」と思ったが、再び 35杯分の仕込みをしておくと、その日の販売個数は 28杯だった。結局、仕込んだうどんは 7杯分が無駄になってしまい、350円ほど損をしてしまった。
3日目は確かに AI の指示通り 30杯分の仕込みをしていれば、損失は 2杯分の 100円で済んだのだが、2日目は AI の指示通りにしていたとしたら、本来儲かったはずの 600円は得られないことになる。どうしたらよかったのか?
その後、このソフトウェアの担当のデータサイエンティストに相談してみると、このソフトウェアは確かに一番誤差の少ない予測ができているのだという。しかし、その後もこの AIの予測はズレまくった。
あなたはこのソフトウェアを信用すべきだろうか??
このソフトウェアの問題点
結論を先に話してしまうと、実はこのソフトウェアは正しい需要予測を行うことができているし、実際性能的には非常に優れている。ただ、残念なことに、このソフトウェアの機能と店主の要望がマッチしているか?というと、そうとは言えない。
なぜならば、この店主の知りたかったのは「何杯のうどんを仕込めば一番儲かるか?」だったのだが、このソフトウェアが目的としていたのは「精度の高い需要予測」だったからだ。つまり、要望と機能にズレがあるのだ。
では、どうすればこの店主の要望を満たすことができたのか?
それには、実は「期待値」という概念が必要になってくる。この「期待値」という言葉はあまり聞いたことがない方もいるかもしれないが、要するに「うどんを N 杯仕込んだときにいくらぐらい儲かりそうか?」という「期待感」を数値で表したものになっている。
そして、この「期待値」を計算するためには、実は「予測分布」というものが必要になる。これはうどんが 1杯売れる未来、2杯売れる未来、…、100杯売れる未来というのを確率値として表現したものになっている。
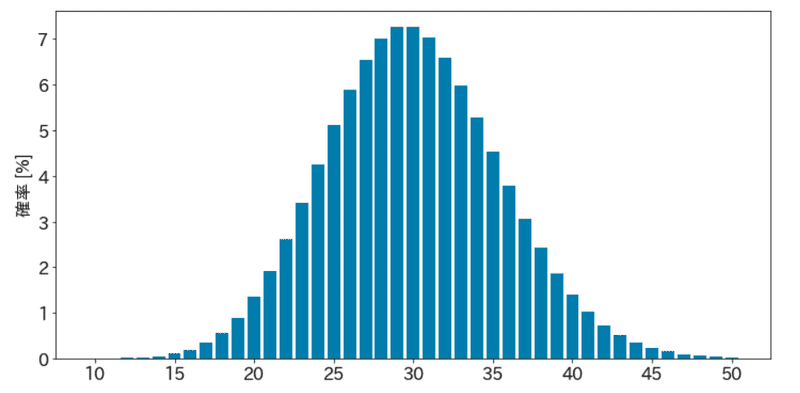
そして、この確率分布をもとに、例えばうどんを 30杯分仕込んでおいたら、平均的にどれくらい儲かりそうか?というのを計算させることができるのだが、この平均的な利益のことを「期待値」と呼んでいる。
例えば、うどんの販売個数の予測分布が上のような感じになったとすると、利益の「期待値」は具体的に数値で計算することができる。例えば、うどんを 30杯仕込んだ場合だと、その期待値は大体 8237円くらいになる(細かな計算は省略)。
そして、この「期待値」を 「1杯分だけ仕込んだ場合」、「2杯分だけ仕込んだ場合」、…とさまざまな行動パターンで計算していくと、結果的に行動パターン毎の「利益の期待値」が計算できるのだが、その「利益の期待値」が最大となる行動を取れば、それが最も儲かるアクションであることがわかる。実際に、いまの場合にこの「利益の期待値」を計算してみると、次のような感じになる。
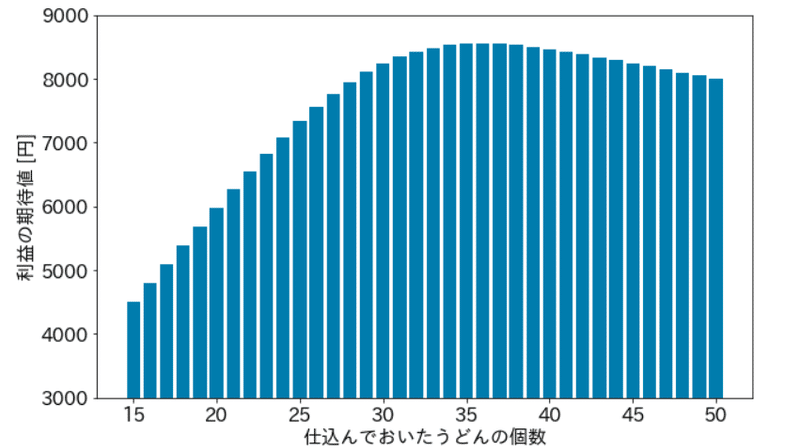
先の予測分布ではピークが 30杯のところにあったことに注意して欲しい。つまり、先の予測分布では確率値が最も大きいのが 30杯だったのが、利益の期待値のピークがあるところは 35杯とか 36杯とかへズレてしまっていることがわかる。
先の店主は、AI が予測した 30杯という予測よりも少し多めの 35杯のうどんを仕込んでおいたのだが、実はこれが悪くない判断だったことがわかる。
ただ、こうした「期待値」を計算させるためには、需要のピンポイントな予測だけでなく、需要のバラツキ(つまり分布)を予測させる必要があり、そうした予測のできないアルゴリズムだと、最終的にこうした「期待値」の計算が難しくなってしまう。
特に、規模の小さな店舗での需要はバラツキが大きいことが知られており、単なるピンポイントな予測は外れることが多いので、利益の最大化という観点からはあまり良い予測とは言えないだろうと考えている。
特に、いまのように損失の非対称性が強い場合は注意が必要で
■ 機会損失(需要を過少に見積もった場合の損失):うどん1杯あたり 300円
■ 廃棄ロス(需要を過大に見積もった場合の損失):うどん1杯あたり 50円
「利益の期待値を最大化させるうどんの仕込み量」は単なる「需要の予測値」のから大きくズレてしまうことが多い。
つまり、この場合だと、実際の需要の予測値よりも多めにうどんを仕込んでおいた方が最終的な儲けは大きくなる、ということなのだが、実際に「何杯分くらい仕込んでおくのが最適なのか?」を正確に計算するためには、どうしても「期待値」という概念が必要になってくる。そして、その「期待値」を計算するために、分布による需要予測が必要となってくる。
分布による需要予測
一般的には、先の分布で言えば、分布の頂点に当たる部分を精度よく推定できることが重視されがちなのだけど、実際にはこの分布の頂点がどこかよりも重要な情報がある。
それは、次の2つの情報だ。
・この確率分布がどれくらい広がっているか?
・損失の非対称性がどれくらい強いか?
この2つの情報がわかっていない場合、結局のところ何杯分のうどんを仕込んでおけばよいのかを正確に決めることはできない、ということになる。
どんなに凄いアルゴリズムで精度良く分布の頂点を予測することができても、損失の非対称性が強ければ、最適な仕込み量はどんどんズレて行ってしまうのだ。
モデルを複雑にすればバラツキは小さくできるのでは?
確かに、こうした認識は間違ってはいない。どこかにモデルに取り込めていない特徴量があり、それを取り込むことで精度が上がっていくことは十分に考えられるのだが、そこにも限界がある。
というのも、こうした来店客数のようなデータの場合は、そもそものデータの発生メカニズムとして、ポアソン分布に従うことが多いからだ。

上はコンビニへの来店客数がどう決まるか?をイメージした図なのだが、実際のところ、このコンビニへの来店客数はおそらくあまり精度よく予測することはできない。もし正確に予測しようとすると、具体的に「誰がいつコンビニに行きたくなっているか?」を正確に予測できないといけないからだ。ただ、そんなことを予測できる特徴量は存在するだろうか?ちょっと考えてみて欲しい。おそらく、なかなかないのではないだろうか…
コストを無制限にかけてよければ、そうしたことができる可能性もあるかもしれないが、現実的には難しいだろうと考えている。
だとすると、具体的に誰がいつコンビニに行きたくなっているかを予測することは諦めないといけないのだが、実際には誰だかはわからないがコンビニに行きたい人は何人かおり、最終的にコンビニに来た来店客数だけは観測できる。そこで、その来店客数を集計すると、その数値がポアソン分布に従うという訳なのだ。
ただ、ポアソン分布は正規分布などとは異なり、分散が平均と一致するような分布になっているため、自動的に分散の大きな分布になってしまう。
そして、この分散をもっと小さくしようとすると、このデータはどこかから来店する誰かではなく、具体的に個人を特定した上で、行動を予測する…みたいなことが必要になってくる。ただ、そもそも人間の未来の行動を正確に予測できるようなアルゴリズムがうまく作れるか?というと、技術的にもコスト的にもあまりうまく行きそうにないので、諦めた方がよいのではないか?と個人的には考えている。
つまり、わからないことはわらかないまま、現実社会をモデル化することで、少しでもデータによる未来予測が世の中の役に立つようになるような時代が来ればいいな…ということで、確率分布をモデルに組み込むことのできる統計モデリングに魅力を感じているのだが、皆さんはどう思われるだろうか??

