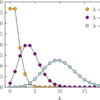
小さな店舗の需要予測が難しい理由
小さな店舗の需要予測は基本的に難しいのではないか?と思っている。それは、店舗への来店客数みたいなものはポアソン分布に従うことが多いからだ。
ポアソン分布というのは、一般の方にはあまり耳慣れない分布かもしれないが、これは実は有名な確率分布で、意外にいろいろな場面で発生する。
店舗への来店客数のようなものもそうだし、交差点を通過する車の台数みたいなものも、ポアソン分布に従うことが多い。さまざまなデータが実はポアソン分布のような分布に従って発生している。

但し、この確率分布は、ガウス分布などとは異なり、連続な変数に対しては使われない。あくまで、この確率分布が対象とするのは、1, 2, 3, 4 … と数えられるデータ、カウントデータと呼ばれるタイプのデータだ。
また、この確率分布の特徴としてよく挙げられるのは、「平均と分散が等しい」という点だ。正規分布などとは異なり、平均と分散を別々にコントロールすることはできない。平均を定めてしまうと、分散も自動的に決まってしまう。平均が小さいときは、分散も小さいが、平均が大きくなると、分散も大きくなる。

…ということは、なんとくなく規模が大きくなればなるほど、データのバラツキが大きくなるように感じてしまうが、実はこれはあくまで絶対的な分散の値が大きくなるという意味で、実際にはポアソン分布に従うデータは規模が大きくなるほどに扱いやすくなる。
なぜならば、相対的なバラツキはポアソン分布の平均値が大きくなるほどに小さくなるからだ。これは簡単な乱数の実験で試してみることもできる。
以下は、2種類の平均値の異なるポアソン乱数を平均値で割ったときのグラフだが、平均値が大きくなるほどに実は相対的な揺らぎが小さくなっていることがわかる(平均が10のときのポアソン乱数と平均が1000のときのポアソン乱数の比較)。
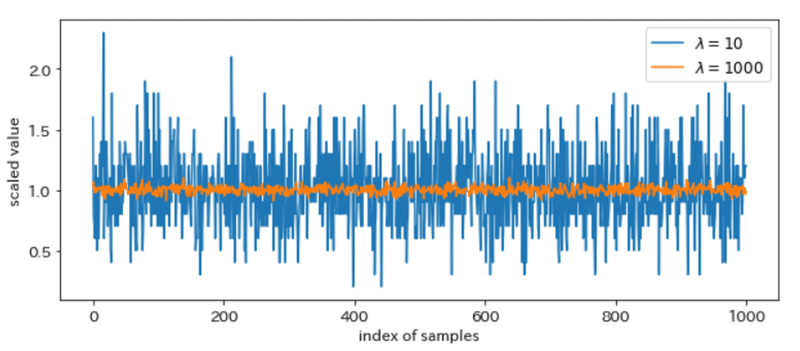
つまり、平均値が大きくなるほどにデータの相対的な揺らぎは小さくなる。
「平均と分散が等しい」と聞くと、なんとなく平均が大きくなるにつれてバラツキも大きくなるように感じてしまうが、実は平均の小さなポアソン分布の方が相対的なバラツキは大きくなる。
結果として、大きな店舗の需要予測は比較的容易で、小さな店舗の需要予測は比較的難しい、といったことが起こる。大規模なショッピングモールの来店者数を予測することは比較的易しくても、小さなコンビニへの来店者数を予測することは難しいのだ。
「小さな店舗の需要予測ぐらい簡単でしょ?」と思う人も多いかもしれないが、実際にはその反対で、小さな店舗の需要の方が揺らぎが大きく、予測精度を出すのは一般的に難しい。
おそらく、このような状況下では、どのような機械学習のアルゴリズムを使って、どのような特徴量を持ってきたとしても、精度の高い予測をするのは難しいのではないかと思っている。なぜならば、そもそものデータの発生原理そのものがデータの本質的なバラツキを生み出しているからだ。
Wikipedia によれば、「稀にしか起こらないような現象を大量に観測した結果がポアソン分布に従う例は極めて多く見られる」とのことだが、こうしたメカニズムに沿って発生するデータはおそらくたくさんある。
そして、そのデータの平均値が小さいとき、その相対的なばらつきは非常に大きくなってしまう。つまり、予測は難しくなるのだ。同じ野菜を売っていても、商店街の小さな八百屋よりも、大きなスーパーの方が有利なのは、背後にこういったメカニズムも働いているのではないか?と密かに思っている。大規模な店舗では、需要予測がし易いので、期限切れで廃棄したり、値引きしたりする商品の量を少なくできるためだ。
小さな店舗の需要予測は諦めた方がよいのか?
基本的には、小さな店舗の需要予測において精度を出すことは難しいが、いくつかの場合では比較的精度の高い予測ができる場合がある。
需要の発生源がうまく特定できるような場合だ。
例えば、大きな野球場の近くにあるラーメン屋などであれば、試合の開催日かどうかで来店者数は増減するだろうし、観光地のホテルに隣接する食堂などであれば、ホテルの宿泊者数に応じて来店者数は増減するだろう。
こうした大きな需要の発生源が特定でき、データが取得できるケースでは、比較的精度の高い予測ができる場合もあり得る。しかし、そうでない場合は基本的に精度の高い予測は難しいことが多い。
例えば、以下のコンビニのように、近隣に住む住民がなんとなく集まってきて来店する、という場合はデータはポアソン分布に従ってしまうので、実際の来店客数はどうしても大きくばらついてしまう(需要の発生源が特定しにくい)。

では、需要予測自体を諦めた方がよいのか?というと、そうとも言い切れない。
無論、精度の高い予測自体は難易度が高いことに変わりはないのだが、予測精度を目標にするのではなく、目標を切り替えてしまうことでも、この問題は回避することができる。
つまり、予測精度自体を目標にするのではなく、例えば利益を最大化することを目標にする、という風に目標を切り替えてしまう。そして、このタイプのアプローチにおいて重要になってくるのが、「需要を分布として予測する」という考え方だ。
需要を分布として予測することで、来店者数が多かった場合、少なかった場合、と場合に分けて利益を算出し、例えば仕入れの食材の量やスタッフの数などを最適な値に決定することが可能となる。これが「ベイズ決定」と呼ばれる考え方だ。
分布による需要予測
こうしたデータによる需要予測、特に分布による予測を強くサポートしてくれる手法のひとつが、統計モデリングとなっている。統計モデリングの世界では、予測は基本的に「事後予測分布」と呼ばれる確率分布により行われる。そして、この「事後予測分布」を使うことで、未来に起こるさまざまな可能性を定量的に見積ることができるようになる。
従来、この分野の知識を身につけるためには、複数の専門書を読んだり、Stan と呼ばれる C言語に似たコードの書き方を身につける必要があり、学習するためのハードルも少し高めだったが、近年 PyMC3 / NumPyro といった新しいツールが登場し、こうした分野も段々と身近なものになってきているので、ぜひトライしてみて欲しい。