Variational Autoencoder の実装 – NumPyro & Haiku

2022年12月3日

概要

NumPyro の公式サイトにある Variational Autoencoder (VAE) の例題を少しだけ改造して、Google Colab 等で動かしてみました。

VAE の実装のためには NumPyro だけでなく、ニューラルネットを実装するライブラリが必要になるのですが、今回は Haiku と呼ばれる DeepMind の開発したライブラリを使ってみています。公式サイトのコードでは、ニューラルネットの実装には stax と呼ばれる JAX に標準で含まれているライブラリを使っているのですが、今回はこの部分を少しだけアレンジしています。

また、今回のコードはデータに MNIST を使いますので、実際にコードを動かす場合には、事前に以下などからデータをダウンロードしておいて下さい。

Install Packages

Google Colab 上で動かすことを前提に説明を進めます。まずは、NumPyro と Haiku のインストールを行います。

!pip install numpyro==0.8.0
!pip install dm-haiku==0.0.5

Import Packages

次に、必要なパッケージをインポートします。

import os
import gzip
import struct
import time

import numpy as np
import matplotlib.pyplot as plt

import jax
import jax.numpy as jnp
from jax import jit, lax

import numpyro
import numpyro.distributions as dist

import haiku as hk
from numpyro.contrib.module import haiku_module

実行環境をセットします。GPU での高速化を試したいときには、下の 'cpu’ の部分を 'gpu’ に置き換えて下さい。

numpyro.set_platform('cpu') # define 'gpu' for GPU
jax.devices()
plt.rcParams['font.size'] = 12
plt.rcParams['figure.figsize'] = [8, 6]

Define Parameters

コードの実行に必要なパラメータを定義します。

DATA_DIR = './'

Z_DIM = 50
HIDDEN_DIM = 400
OUT_DIM = 28 * 28

NUM_EPOCHS = 100
BATCH_SIZE = 256
LEARNING_RATE = 0.001

Load MNIST

MNIST のデータのロードの部分に関しても、少しだけ手を加えています。元々のコードではデータのロード部分がパッケージの中に含まれてしまっていて、かなり「サラッ」と書いてあるのですが、実はこの部分も大いに高速化に貢献していて、実は重要な部分ではないかと思っています。そこで、こちらの記事では、このデータロードの部分も敢えて外出ししています。

基本的には画像データをメモリ上にロードして、データを小分けして読み出すような関数を定義しているだけなのですが、この「メモリからのデータの読み出し」の部分にも JAX の関数が使われており、JIT による高速化の恩恵が受けられるようになっているところがポイントです。

ちなみに、PyTorch の DataLoader を使ってこの部分を書き換えてみたりもしたのですが、その際には実行速度が大きく落ちてしまいました…

fname_train_images = os.path.join(DATA_DIR, 'train-images-idx3-ubyte.gz')
fname_train_labels = os.path.join(DATA_DIR, 'train-labels-idx1-ubyte.gz')
fname_valid_images = os.path.join(DATA_DIR, 't10k-images-idx3-ubyte.gz')
fname_valid_labels = os.path.join(DATA_DIR, 't10k-labels-idx1-ubyte.gz')
def read_image(file):

    with gzip.open(file, "rb") as f:

        _, _, nrows, ncols = struct.unpack(">IIII", f.read(16))

        data = np.frombuffer(f.read(), dtype=np.uint8) / np.float32(255.0)

        return data.reshape(-1, nrows, ncols)
def read_label(file):

    with gzip.open(file, "rb") as f:

        f.read(8)

        data = np.frombuffer(f.read(), dtype=np.int8)

        return data
train_images = jax.device_put(read_image(fname_train_images))
train_labels = jax.device_put(read_label(fname_train_labels))
valid_images = jax.device_put(read_image(fname_valid_images))
valid_labels = jax.device_put(read_label(fname_valid_labels))
def in_memory_data_loader(images, labels, batch_size=1, shuffle=False):

    num_records = len(labels)

    idxs = np.arange(num_records)    
    idxs = np.random.permutation(idxs) if shuffle else idxs

    num_batch = num_records // batch_size

    images = images.reshape(images.shape[0], -1)
    images = (images > 0.5).astype(jnp.float32)

    def fetch(k):

        ret_idx = lax.dynamic_slice_in_dim(idxs, k * batch_size, batch_size)

        batch_image = lax.index_take(images, (ret_idx,), axes=(0,))
        batch_label = lax.index_take(labels, (ret_idx,), axes=(0,))
        
        return batch_image, batch_label

    return num_batch, fetch
num_batch_train, train_fetch = in_memory_data_loader(train_images, train_labels, batch_size=BATCH_SIZE)
num_batch_valid, valid_fetch = in_memory_data_loader(valid_images, valid_labels, batch_size=BATCH_SIZE)

少しややこしい感じがしますが、基本的には画像データをメモリ上に読み込み、データを小分けして読み出しているだけです。個人的には、バッチを読み出す関数 fetch を戻り値として返すあたりが、ちょっとトリッキーな感じがしています。「一旦保持したデータを小分けして読み出す」という意味ではクラスの方が向いているのではないかと一瞬考えたのですが、試しにクラスで実装してみるとやはり少しオーバヘッドが増えてしまいました。

なお、元々のコードはこちらから参照することができます。上のコードは、こちらの load_dataset という関数の中身を少しシンプルに書き直したものになっています。

Define Encoder and Decoder

それでは、これから VAE の実装に入ってきます。まずは、以下のような感じで VAE の Encode側と Decode側をそれぞれ Haiku でコード化します。Haiku によるネットワークの実装方法はここでは細かく解説はしませんが、VAE のネットワークはそれほど複雑なものではないので、下のコードの方からなんとか類推して頂けましたら幸いです。

class HaikuEncoder:

    def __init__(self, hidden_dim, z_dim):

        self._hidden_dim = hidden_dim
        self._z_dim = z_dim
    
    def __call__(self, x):

        x = hk.Linear(self._hidden_dim)(x)
        x = jax.nn.softplus(x)

        z_loc = hk.Linear(self._z_dim)(x)
        z_std = jnp.exp(hk.Linear(self._z_dim)(x))

        return z_loc, z_std        
class HaikuDecoder:

    def __init__(self, hidden_dim, out_dim):

        self._hidden_dim = hidden_dim
        self._out_dim = out_dim
    
    def __call__(self, z):

        z = hk.Linear(self._hidden_dim)(z)
        z = jax.nn.softplus(z)
        z = hk.Linear(self._out_dim)(z)
        x = jax.nn.sigmoid(z)

        return x

VAE の実装では、これらの関数を NumPyro のモデルへ組み込んでいくのですが、そのために以下のような２つの変換関数が必要になります。

hk.transform 関数：

haiku_module 関数：

hk.transform 関数は Haiku の関数で、上のように関数で定義したニューラルネットを Haiku のモジュールへ変換していくものになります。Haiku のモジュールの定義の方法は、こうした変換関数を使う方法と hk.Module というクラスを継承してクラスを定義する方法の２通りの方法があるのですが、ここでは hk.transform 関数を使う方法を紹介しています。

また、haiku_module 関数は、このようにして定義した Haiku のモジュール（ニューラルネット）のパラメータを変分推論における最適化の対象として登録をしています。

Define Model

次に、変分推論に必要になる model 関数と guide 関数を定義してゆきます。model 関数の方には、潜在変数から実際の観測データが生成される過程をコード化していきます。

def model(batch, hidden_dim=400, z_dim=100):

    batch_dim, out_dim = jnp.shape(batch)

    haiku_decoder = hk.transform(HaikuDecoder(hidden_dim, out_dim))
    
    decoder = haiku_module('decoder', haiku_decoder, input_shape=(batch_dim, z_dim))
    
    with numpyro.plate('batch', batch_dim):
        
        z = numpyro.sample('z', dist.Normal(0, 1).expand([z_dim]).to_event(1))
        
        img_loc = decoder(z)
        
        numpyro.sample('obs', dist.Bernoulli(img_loc).to_event(1), obs=batch)

NumPyro のコードをある程度見慣れている方にとっては、それほど摩訶不思議なコードには見えないかと思うのですが、おそらく “to_event(1)" という部分が、あまり見慣れない方も多いのではないかと思います。この辺りのことが気になる方は、以下のサイトを参考にして頂くとよいかもしれません…

Define Guide

次に、guide関数を定義します。この関数は純粋に変分推論のために定義されるもので、変分推論で使われる確率分布（変分分布）を定義します。この確率分布 $q_\phi(z|x)$ は、潜在変数の事後分布 $p_\theta(z|x)$ を近似するための分布で、変分推論においては非常に本質的なものになります。

def guide(batch, hidden_dim=400, z_dim=100):

    batch_dim, out_dim = jnp.shape(batch)

    haiku_encoder = hk.transform(HaikuEncoder(hidden_dim, z_dim))

    encoder = haiku_module('encoder', haiku_encoder, input_shape=(batch_dim, out_dim))
    
    z_loc, z_std = encoder(batch)
    
    with numpyro.plate('batch', batch_dim):
        
        numpyro.sample('z', dist.Normal(z_loc, z_std).to_event(1))

変分推論に関しては、日本語で解説しているサイトや書籍も多いので、ぜひ検索してみて下さい。英語でもよければ Pyro の Introduction の部分が参考になるのではないかと思います。

また、VAE の Introduction としては、Kingma 氏の論文が非常に参考になりました。

また、個人的には Blei 先生の次の論文も勉強になりました。

Define Function for Inference

以上までのコードで、モデルの定義ができたので、ここからは実際の推論の準備に入っていきます。パラメータを更新していくための関数（update）と損失（ELBO）を計算する関数（evaluate）を準備します。

ここでの一番のポイントは、svi.update と svi.evaluate という２つの関数です。どちらも変分推論の１ステップ分を実行する関数になりますが、svi.evaulate の方は損失（ELBO）のみを計算する関数になっています。詳細については、こちらを参考にして見て下さい。

@jit
def update(svi_state):

    def body_fn(i, val):
        
        svi_state, loss_sum = val

        batch_image, _ = train_fetch(i)
        
        svi_state, loss = svi.update(svi_state, batch_image)
        
        loss_sum += loss / len(batch_image)
        
        return svi_state, loss_sum

    svi_state, loss_sum = lax.fori_loop(0, num_batch_train, body_fn, (svi_state, 0.0))
    loss_ave = loss_sum / num_batch_train

    return svi_state, loss_ave
@jit
def evaluate(svi_state):
    
    def body_fn(i, loss_sum):
        
        batch_image, _ = valid_fetch(i)
        
        loss = svi.evaluate(svi_state, batch_image)
        
        loss_sum += loss / len(batch_image)
        
        return loss_sum

    loss_sum = lax.fori_loop(0, num_batch_valid, body_fn, 0.0)
    loss_ave = loss_sum / num_batch_valid
    
    return loss_ave

それから、ここではもうひとつポイントがあります。それは JAX による高速化です。Python でのループ処理を高速化するために、fori_loop という関数が使われています。一見難しそうに見えるのですが、この関数を使うには for 文の中身を関数として切り出してやり（body_fn）、その関数を fori_loop に渡してやるだけで OK です。

この for 文の中身の処理がうまく JAX のお気に召す形になっていれば、素晴らしく高速化できるのですが、そうでない場合は謎のエラーメッセージに悩むことになるかもしれません…

Inference

ここまで準備ができていると、次々にバッチを読み出しながら推論を進めていくことができます。今回は、svi.update, svi.evaluate, svi.init などの関数を使って実装を進めましたが、実はこの辺の処理は svi.run という関数でまとめて実行してしまうこともできます。詳細については、こちらを参考にしてみて下さい。

adam = numpyro.optim.Adam(LEARNING_RATE)
svi = numpyro.infer.SVI(model, guide, adam, numpyro.infer.Trace_ELBO(), hidden_dim=HIDDEN_DIM, z_dim=Z_DIM)
batch_image, _ = train_fetch(0)
svi_state = svi.init(jax.random.PRNGKey(0), batch_image)
%%time

losses = np.zeros(NUM_EPOCHS)

for k in range(NUM_EPOCHS):
        
    t_start = time.time()
        
    svi_state, _ = update(svi_state)
    
    losses[k] = evaluate(svi_state).block_until_ready()

    t_end = time.time()
    
    print("Epoch {}: loss = {:.2f} ({:.3f} s)".format(k, losses[k], t_end - t_start))
Epoch 0: loss = 179.34 (5.275 s)
Epoch 1: loss = 150.42 (1.491 s)
Epoch 2: loss = 133.37 (1.490 s)
Epoch 3: loss = 122.64 (1.546 s)

## 中略

Epoch 97: loss = 83.03 (1.433 s)
Epoch 98: loss = 83.02 (1.510 s)
Epoch 99: loss = 83.47 (1.540 s)
CPU times: user 7min 59s, sys: 16.1 s, total: 8min 15s
Wall time: 2min 34s
plt.plot(losses)
plt.xlabel('Epoch')
plt.ylabel('Loss')

plt.tight_layout()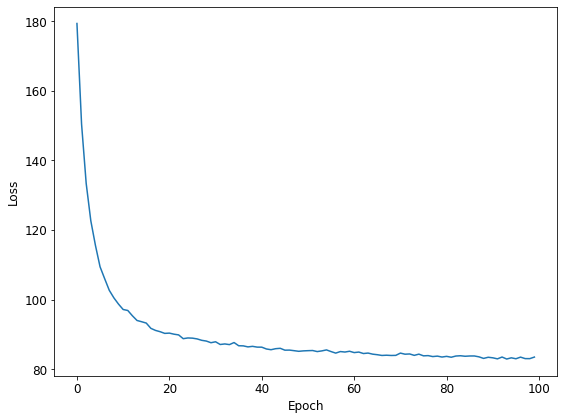

Check Results

最後に画像データを VAE に通して、うまく元の画像に近いものが復元できているか、チェックします。まずは、svi.get_params で svi_state からパラメータを取り出し、後で encoder と decoder のオブジェクトを使う際に使えるように準備しておきます。 

params = svi.get_params(svi_state)

encoder_params = params['encoder$params']
decoder_params = params['decoder$params']

次に、encoder と decoder のオブジェクトを用意します。

encoder = hk.transform(HaikuEncoder(HIDDEN_DIM, Z_DIM))
decoder = hk.transform(HaikuDecoder(HIDDEN_DIM, OUT_DIM))

準備ができたので、これらのネットワークを使って、画像が復元できるかをチェックします。最初のバッチの先頭の５枚の画像についてチェックすることにします。VAE の encoder/decoder には apply という関数を使います（※最初の投稿では下のコードが間違っておりました。お詫びして訂正させて頂きます）。

batch_image, _ = train_fetch(0)

z_loc, z_std = encoder.apply(encoder_params, None, batch_image)

z = dist.Normal(z_loc, z_std).sample(jax.random.PRNGKey(42))

batch_recon = decoder.apply(decoder_params, None, z)
fig, axes = plt.subplots(2, 5, figsize=(10, 3))

for k in range(5):

    axes[0][k].imshow(batch_image[k].reshape(28, 28), 'gray')
    axes[0][k].set_xticks([])
    axes[0][k].set_yticks([])

    axes[1][k].imshow(batch_recon[k].reshape(28, 28), 'gray')
    axes[1][k].set_xticks([])
    axes[1][k].set_yticks([])

Summary

最後に、推論にかかった時間を記しておきます。計測しているのは、%%time で時間を測っているセルのところです。Google Colab と Local Machine の２通りで時間を測っています。Google Colab 上では「GPUあり」の場合の実行時間を計測し、Local Machine では「GPUなし」の場合の実行時間を計測しました。

GPUなし / Local Machine (Intel Core i5-8400) : 2min 34s
GPUあり / Google Colab (Tesla T4) : 0min 18s

GPU により変分推論が大幅に高速化していることがわかります。MCMC のときは、GPU で大幅に高速化する…といったことはあまり経験がなかったので、これは変分推論と GPU の相性の良さを示唆しているような気がします。ただ、「いつでも GPU を使えば、変分推論が高速化するか？」というと、どうもそうではなく、これもモデル次第のようです…

お願い

記事につきましては、間違いないように十分に気をつけて書いたつもりなのですが、どこかで変なことを行っているかもしれません。お気付きの点がありましたら、ご面倒でもお問合せの方からご指摘頂けますと、ありがたいです。

NumPyro,NumPyro【応用編】

Posted by 管理者