WAIC は何を近似しているか?
WAIC に関しては、考案者である渡辺澄夫先生が直接丁寧な解説を提供して下さっているので、これ以上付け足すことはないのですが、蛇足を承知の上でちょっとだけ解説をさせて頂けたらと思います。
WAIC は何を近似しているのか?
WAIC は、次のような「汎化損失」と呼ばれる量を近似するものになっています。
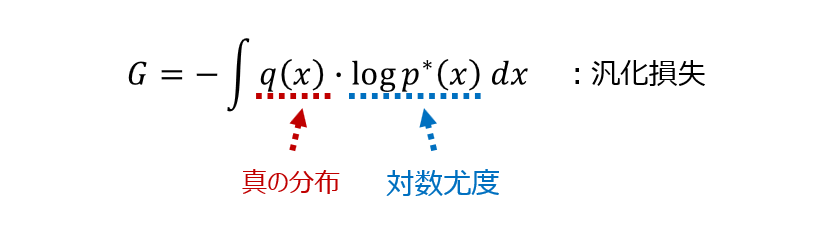
なお、上の式での $p^*(x)$ は事後予測分布(単に予測分布とも呼ばれます)を表しています。
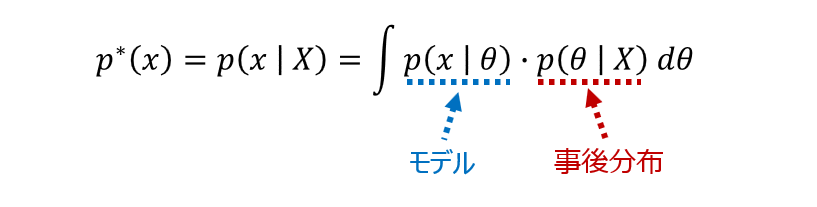
汎化損失は、基本的には $q(x)$ と $p^*(x)$ の違いを測るものになっていますが、この汎化損失を近似しているものが WAIC です。
汎化損失は、その定義に真の分布 $q(x)$ なるものを含んでいるために、直接計算することは難しいことが多い訳ですが、それをちゃんと近似計算できてしまうのが WAIC の凄いところです。
「汎化損失」を理解する
上で「汎化損失」の定義をしましたが、この「汎化損失」についてもう少し補足してみたいと思います。汎化損失は式のままだと、次のような定義な訳ですが
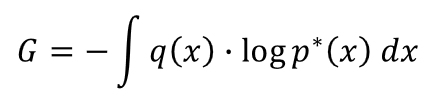
ここで、「真の分布 $q(x)$ から新しく無数のサンプル $\{x_i\}$ が取れる」という状況を想定してみます。現実の世界では、データは真の分布から発生する訳ですから、こうした状況を考えるのは割と自然な考え方です。こうした無数のサンプルを使うと、上の積分は次のように近似的に表現することができます(モンテカルロ近似)。
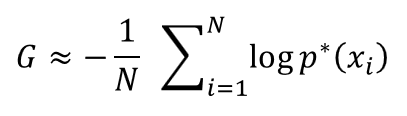
つまり、汎化損失は「真の分布 $q(x)$ から新しく沢山のサンプルを発生させたときに、その対数尤度(事後予測分布への当てはまり具合)を平均したもの」に近くなります。
別の角度から理解する
また、この「汎化損失」は、次のように式変形することができます。

真の分布 $q(x)$ が固定されているときには、エントロピーの部分は定数になりますので、結局この「汎化損失」は真の分布 $q(x)$ と事後予測分布 $p^*(x)$ の違いを測っていることになります。上式では「KL情報量」という部分が2つの分布の違いを測る部分になっています。
WAIC(広く使える情報量基準)とは?
WAIC は、この「汎化損失」を近似計算しています。真の分布 $q(x)$ などという得たいの知れないものを含んでいながら、これをなんとか近似計算できてしまうというのが WAIC の凄いところです。
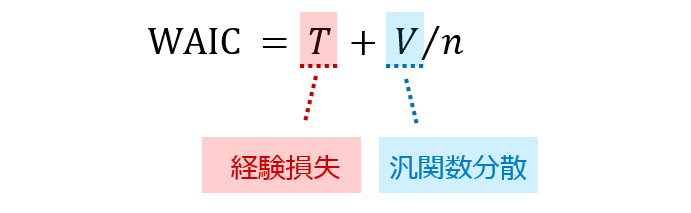
なお、「経験損失」と「汎関数分散」の定義は、次の通りです。
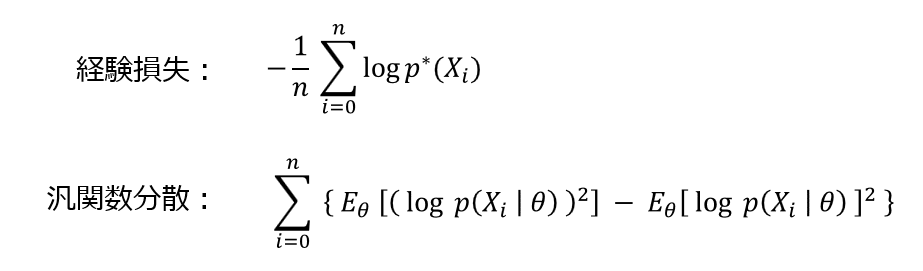
なお、$E_\theta[\cdot]$ は、$\theta$ の事後確率に基づく期待値計算を表しています。
渡辺先生が証明されたのは、一般的な条件のもとで「汎化損失」が「経験損失」と「汎関数分散」と呼ばれるものによって近似的に計算できる…という部分になります。個人的に特に先生の凄いと思うところは、この証明を現代数学のさまざまな道具を持ち込んでやり遂げてしまった…というところで、例えて言うなら「アインシュタインが物理学の中に微分幾何学を持ち込んで一般相対性理論を作り上げてしまった」というのに近いものがあるのではないかと思っています。こうした美しい現代数学と統計の絡みの部分に興味がある方は、ぜひ渡辺先生の本を読んで頂きたいと思うのですが、我々はもうしばらく地上世界に留まってみたいと思います。
用語に関する補足
渡辺先生のサイトをジロジロとみていると、さまざまな情報があり、サイトを見ているだけでもかなり参考になるのですが、海外の書籍や論文を見ると、少し渡辺先生の用語と違っている部分があることがありますので、その辺りを少し補足していきたいと思います。私が PyMC3 を勉強する際に利用させて頂いた Osvaldo Martin という人の書いた次のような教科書があるのですが
この書籍の中では、WAIC に関して次のような定義がなされています。
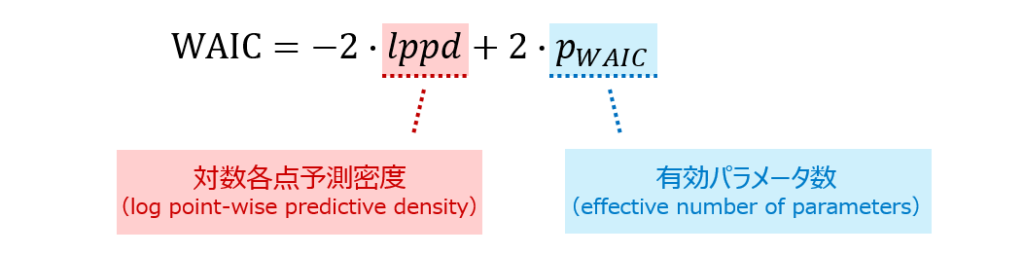
海外の論文などを見ていても、こうした用語が使われていることがあり、ちょっとびっくりするのですが、式の定義をじっと見ると全く新しいものを定義しているのではないことがわかります(「対数各点予測密度」の部分が「経験損失」、「有効パラメータ数」の部分が「汎関数分散」に対応します)。
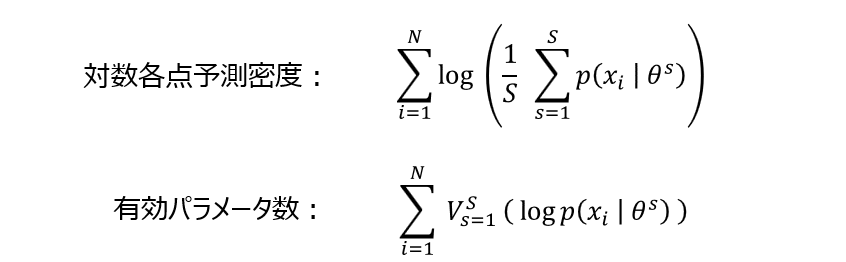
なお、上式において $\theta_1, \theta_2, …, \theta_S $ は、パラメータの事後分布からのサンプルを表し、$V^S_{s=1}(\cdot)$ はサンプル $\{\theta_s\}^S_{s=1}$ による分散の計算を表します。
このように、書籍によって用語が異なっていたり、定数倍がずれていたり…ということがあるのですが、基本的には同じものを表しています。
クロスバリデーションとの関係性
MCMC を使った計算をしていると、もうひとつ PSIS-LOOCV といったものを見かけることがあるかと思います。これも和訳にあまり自信がないのですが、「パレート平滑化 重点サンプリング 1個抜き交差検証」みたいな感じになるのではないかと思います(大丈夫かな??)。

LOOCV(一個抜き交差検証)は、機械学習でよく使われるものですが、この LOOCV を「重点サンプリング」と呼ばれる方法により近似計算しているものが PSIS-LOOCV になります。
経験上、WAIC と PSIS-LOOCV はかなり近い値を取ることが多いのですが、たまに Arviz などで計算させている際にたくさんワーニングが出ているようなときには、これらの値がズレることがあります。「どっちがいいの?」と考えると、いろいろと難しそうなのですが、幸い両方とも簡単に計算できるので、私はなるべく両方を計算させて、ワーニングが出るようなときには結果を注意してみるようにしています(能力的にそれくらいしかできない…)。
この辺りの議論が気になる方は、渡辺先生の解説を読まれるか
ゲルマン先生の論文を読まれるのがよいのではないかと思います。
https://arxiv.org/pdf/1507.04544.pdf
Arviz による WAIC の計算
Python では、Arviz というパッケージを使うと、WAIC も PSIS-LOOCV も非常に簡単に計算できます。

PSIS-LOOCV の方は、上の az.waic を az.loo に置き換えると計算できます。idata は、InferenceData オブジェクトと呼ばれる Arviz のオブジェクトです。また、スケールに関するオプションは次の通りです。

基本的にはモデルの選択に使うことが多いので、絶対的な値…というよりは、大小に興味があるのですが、定義により符号がひっくり返ることがあるので、注意が必要です。
WAIC の面白い使い方
WAIC と言うと、基本的には「モデル選択に使うもの」…という認識だったのですが、WAIC は実はデータ点ごとに計算していくことができまして、この特徴を使うと更にデータ分析の幅を広げてゆくことができます。
上の動画は、Richard McElreath さんという非常に有名な先生のオンライン動画なのですが、この動画の 58:00 あたりから2つのモデルでの WAIC の差を使ってデータ分析を進める…というようなことをやっています。
この Richard McElreath 先生は、もともと「進化人類学」なる分野の先生らしいのですが、統計学を実際のデータに適用していくという観点から、非常にわかりやすいコンテンツをいろいろ整備されています。先生の一番有名な本は、おそらくこちらの Statistical Rethinking という本です。
こちらの書籍の例題は、Stan だけでなく、さまざまな確率プログラミングのパッケージで実装されており、この教科書が海外ではとってもメジャーな教科書であることが見て取れます。
ずっとどこかの偉い先生が翻訳してくれないかな…と思っているのですが、なかなか出てきませんね。
おわりに
WAIC に関しては、渡辺先生が詳しい解説記事を上げて頂いているので、そちらの記事を見て頂くのが一番間違いないとは思うのですが、今回力不足を承知で記事を書いてみました。
一応、間違いがないように気をつけて書いたつもりなのですが、どこかで変なことを言っているかもしれません。お気付きの点がありましたら、ご面倒でもお問合せの方からご指摘頂けますと、ありがたいです。